plot(mfdat)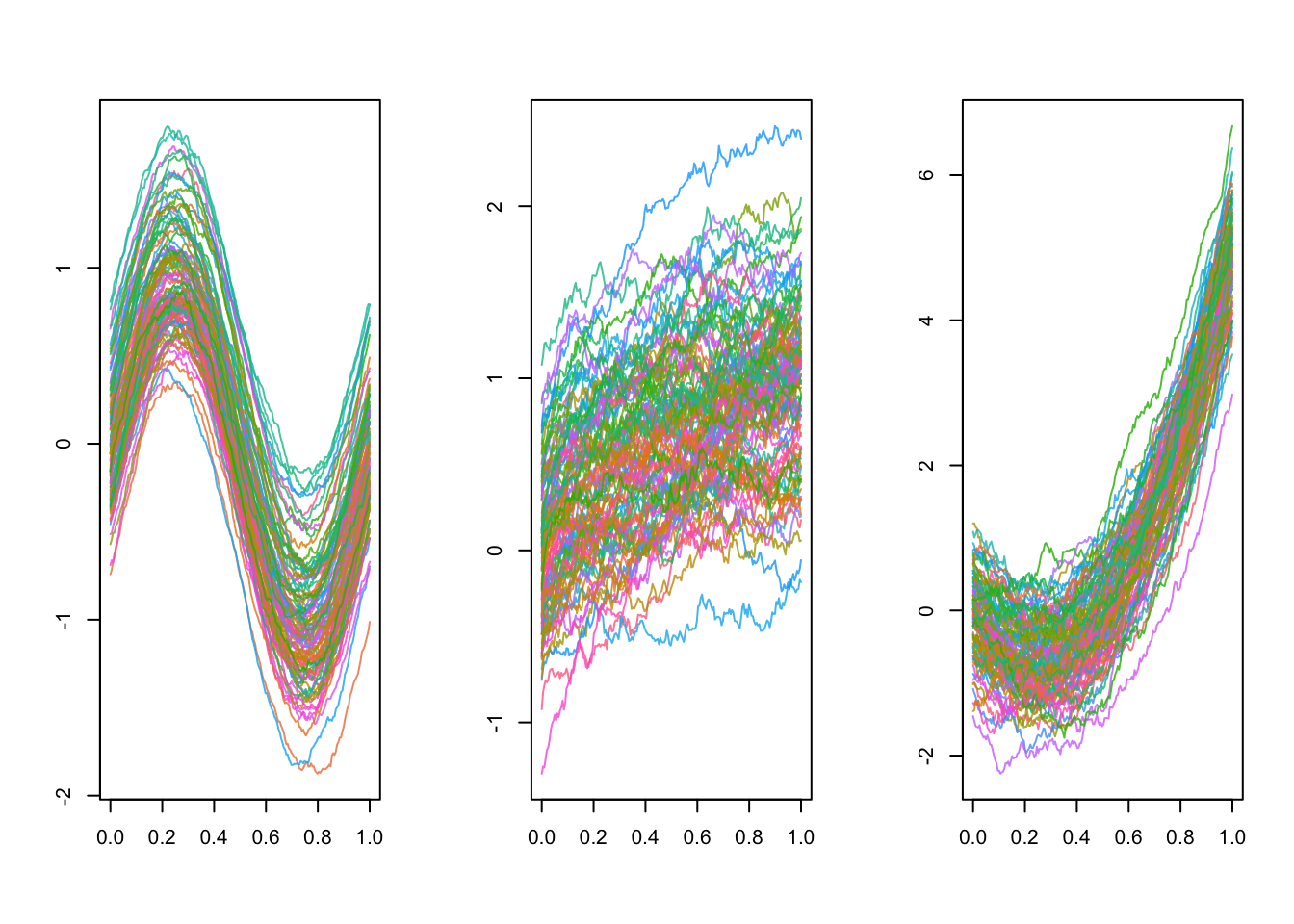
Aymeric Stamm
We have simulated 3D functional data for this lab that is provided in the Quarto document in the dat object.
The dat object is a list of size \(100\) containing \(100\) three-dimensional curves observed on a common grid of size \(200\) of the interval \([0, 1]\).
As a result, each element of the dat list is a \(3 \times 200\) matrix.
Here we focus on a subset of the data, the first \(21\) curves, which looks like:
The goal is to implement a function similar to stats::dist() which computes the pairwise distance matrix on this functional dataset using the Hausdorff distance.
We can implement the Hausdorff distance between two curves as:
This version exploits the vectorized nature of R to compute the Hausdorff distance via calls to colSums() and max(). Another version based on a double loop is provided by the following hausdorff_distance_for() function:
hausdorff_distance_for <- function(x, y) {
P <- ncol(x)
dX <- 0
dY <- 0
for (i in 1:P) {
min_dist_x <- Inf
min_dist_y <- Inf
for (j in 1:P) {
dist_x <- sum((y[, j] - x[, i])^2)
if (dist_x < min_dist_x) {
min_dist_x <- dist_x
}
dist_y <- sum((x[, j] - y[, i])^2)
if (dist_y < min_dist_y) {
min_dist_y <- dist_y
}
}
if (min_dist_x > dX) {
dX <- min_dist_x
}
if (min_dist_y > dY) {
dY <- min_dist_y
}
}
sqrt(max(dX, dY))
}We can benchmark the two versions:
Expression |
Median computation time |
Memory allocation |
|---|---|---|
| hausdorff_distance_vec(dat[[1]], dat[[2]]) | 2.02 ms | 2.7 MB |
| hausdorff_distance_for(dat[[1]], dat[[2]]) | 50.08 ms | 124.6 kB |
We conclude that the vectorized version is faster but has a huge memory footprint compared to the loop-based version. This means that the vectorized version is not suitable for even moderately large data sets.
Take a look at the documentation of the stats::dist() function to understand how to make an object of class dist.
We can exploit the previous functions to compute the pairwise distance matrix using the Hausdorff distance:
dist_r_v1 <- function(x, vectorized = FALSE) {
hausdorff_distance <- if (vectorized)
hausdorff_distance_vec
else
hausdorff_distance_for
N <- length(x)
out <- 1:(N - 1) |>
purrr::map(\(i) {
purrr::map_dbl((i + 1):N, \(j) {
hausdorff_distance(x[[i]], x[[j]])
})
}) |>
purrr::list_c()
attributes(out) <- NULL
attr(out, "Size") <- N
lbls <- names(x)
attr(out, "Labels") <- if (is.null(lbls)) 1:N else lbls
attr(out, "Diag") <- FALSE
attr(out, "Upper") <- FALSE
attr(out, "method") <- "hausdorff"
class(out) <- "dist"
out
}We can benchmark the two versions:
Expression |
Median computation time |
Memory allocation |
|---|---|---|
| dist_r_v1(dat, vectorized = TRUE) | 0.48 s | 546.5 MB |
| dist_r_v1(dat, vectorized = FALSE) | 11.18 s | 3 kB |
We confirm that the vectorized version is not scalable to large datasets. Using it on the full dataset actually requires 12GB of memory! We will therefore focus on the loop-based version from now on.