Performs hierarchical clustering for functional data with amplitude and phase separation
Source:R/fdahclust.R
fdahclust.RdThis function extends hierarchical agglomerative clustering to functional data. It includes the possibility to separate amplitude and phase information.
Usage
fdahclust(
x,
y = NULL,
n_clusters = 1L,
is_domain_interval = FALSE,
transformation = c("identity", "srvf"),
warping_class = c("none", "shift", "dilation", "affine", "bpd"),
centroid_type = "mean",
metric = c("l2", "normalized_l2", "pearson"),
cluster_on_phase = FALSE,
linkage_criterion = c("complete", "average", "single", "ward.D2"),
use_verbose = FALSE,
warping_options = c(0.15, 0.15),
maximum_number_of_iterations = 100L,
number_of_threads = 1L,
parallel_method = 0L,
distance_relative_tolerance = 0.001,
use_fence = FALSE,
check_total_dissimilarity = TRUE,
compute_overall_center = FALSE
)Arguments
- x
A numeric vector of length \(M\) or a numeric matrix of shape \(N \times M\) or an object of class
funData::funData. If a numeric vector or matrix, it specifies the grid(s) of size \(M\) on which each of the \(N\) curves have been observed. If an object of classfunData::funData, it contains the whole functional data set and theyargument is not used.- y
Either a numeric matrix of shape \(N \times M\) or a numeric array of shape \(N \times L \times M\) or an object of class
fda::fd. If a numeric matrix or array, it specifies the \(N\)-sample of \(L\)-dimensional curves observed on grids of size \(M\). If an object of classfda::fd, it contains all the necessary information about the functional data set to be able to evaluate it on user-defined grids.- n_clusters
An integer value specifying the number of clusters. Defaults to
1L.- is_domain_interval
A boolean specifying whether the sample of curves is defined on a fixed interval. Defaults to
FALSE.- transformation
A string specifying the transformation to apply to the original sample of curves. Choices are no transformation (
transformation = "identity") or square-root velocity functiontransformation = "srvf". Defaults to"identity".- warping_class
A string specifying the class of warping functions. Choices are no warping (
warping_class = "none"), shifty = x + b(warping_class = "shift"), dilationy = ax(warping_class = "dilation"), affiney = ax + b(warping_class = "affine") or boundary-preserving diffeomorphism (warping_class = "bpd"). Defaults to"none".- centroid_type
A string specifying the type of centroid to compute. Choices are
"mean","median""medoid","lowess"or"poly". Defaults to"mean". If LOWESS appproximation is chosen, the user can append an integer between 0 and 100 as in"lowess20". This number will be used as the smoother span. This gives the proportion of points in the plot which influence the smooth at each value. Larger values give more smoothness. The default value is 10%. If polynomial approximation is chosen, the user can append an positive integer as in"poly3". This number will be used as the degree of the polynomial model. The default value is4L.- metric
A string specifying the metric used to compare curves. Choices are
"l2","normalized_l2"or"pearson". Iftransformation == "srvf", the metric must be"l2"because the SRVF transform maps absolutely continuous functions to square-integrable functions. Iftransformation == "identity"andwarping_classis eitherdilationoraffine, the metric cab be either"normalized_l2"or"pearson". The L2 distance is indeed not dilation-invariant or affine-invariant. The metric can also be"l2"ifwarping_class == "shift". Defaults to"l2".- cluster_on_phase
A boolean specifying whether clustering should be based on phase variation or amplitude variation. Defaults to
FALSEwhich implies amplitude variation.- linkage_criterion
A string specifying which linkage criterion should be used to compute distances between sets of curves. Choices are
"complete"for complete linkage,"average"for average linkage and"single"for single linkage. Seestats::hclust()for more details. Defaults to"complete".- use_verbose
A boolean specifying whether the algorithm should output details of the steps to the console. Defaults to
FALSE.- warping_options
A numeric vector supplied as a helper to the chosen
warping_classto decide on warping parameter bounds. This is used only whenwarping_class != "srvf".- maximum_number_of_iterations
An integer specifying the maximum number of iterations before the algorithm stops if no other convergence criterion was met. Defaults to
100L.- number_of_threads
An integer value specifying the number of threads used for parallelization. Defaults to
1L. This is used only whenwarping_class != "srvf".- parallel_method
An integer value specifying the type of desired parallelization for template computation, If
0L, templates are computed in parallel. If1L, parallelization occurs within a single template computation (only for the medoid method as of now). Defaults to0L. This is used only whenwarping_class != "srvf".- distance_relative_tolerance
A numeric value specifying a relative tolerance on the distance update between two iterations. If all observations have not sufficiently improved in that sense, the algorithm stops. Defaults to
1e-3. This is used only whenwarping_class != "srvf".- use_fence
A boolean specifying whether the fence algorithm should be used to robustify the algorithm against outliers. Defaults to
FALSE. This is used only whenwarping_class != "srvf".- check_total_dissimilarity
A boolean specifying whether an additional stopping criterion based on improvement of the total dissimilarity should be used. Defaults to
TRUE. This is used only whenwarping_class != "srvf".- compute_overall_center
A boolean specifying whether the overall center should be also computed. Defaults to
FALSE. This is used only whenwarping_class != "srvf".
Value
An object of class caps.
Details
The number of clusters is required as input because, with functional data, once hierarchical clustering is performed, curves within clusters need to be aligned to their corresponding centroid.
Examples
#----------------------------------
# Extracts 15 out of the 30 simulated curves in `simulated30_sub` data set
idx <- c(1:5, 11:15, 21:25)
x <- simulated30_sub$x[idx, ]
y <- simulated30_sub$y[idx, , ]
#----------------------------------
# Runs an HAC with affine alignment, searching for 2 clusters
out <- fdahclust(
x = x,
y = y,
n_clusters = 2,
warping_class = "affine",
metric = "normalized_l2"
)
#----------------------------------
# Then visualize the results
# Either with ggplot2 via ggplot2::autoplot(out)
# or using graphics::plot()
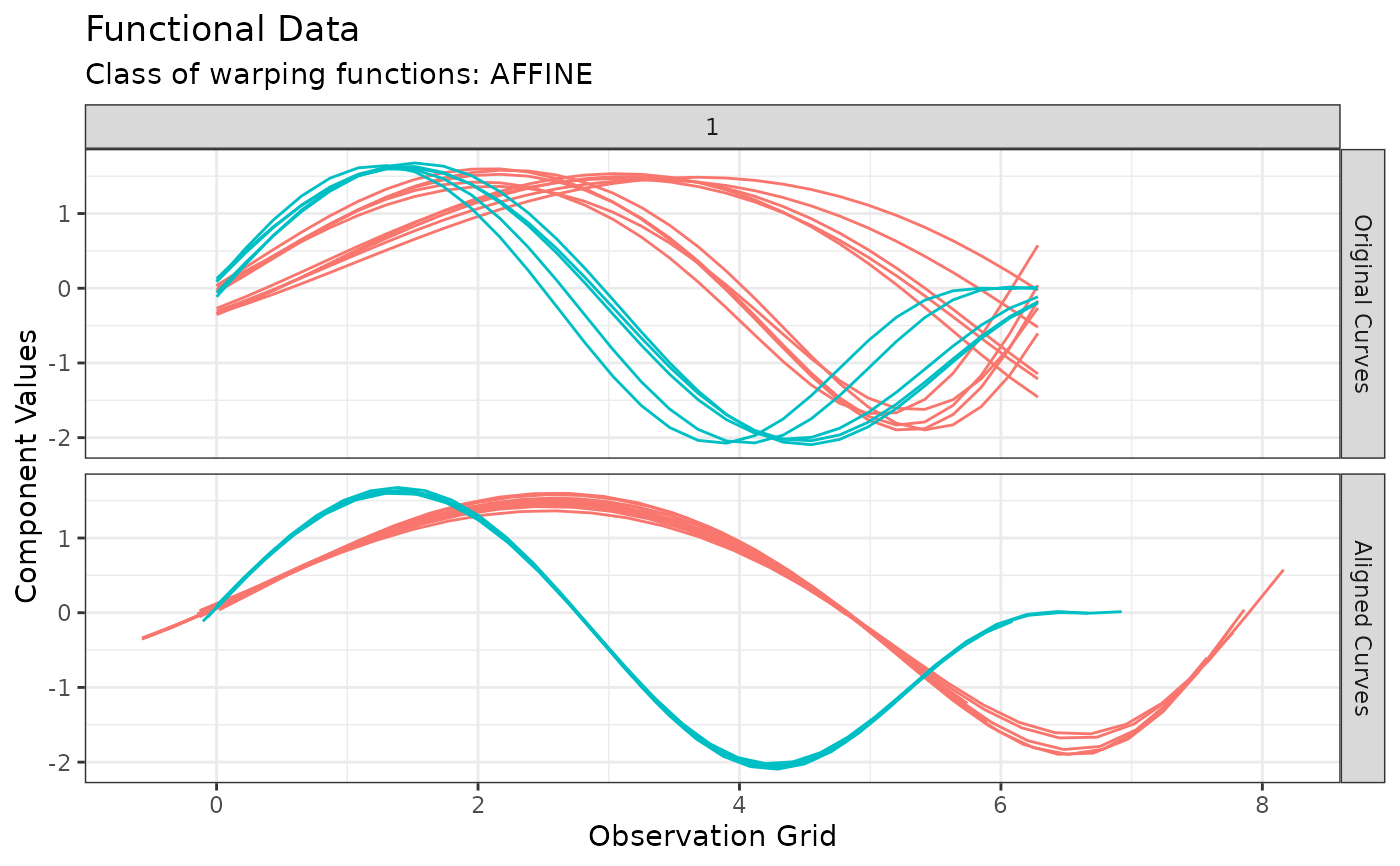
# You can visualize the original and aligned curves with:
plot(out, type = "amplitude")
#> Warning: row names were found from a short variable and have been discarded
#> Warning: row names were found from a short variable and have been discarded
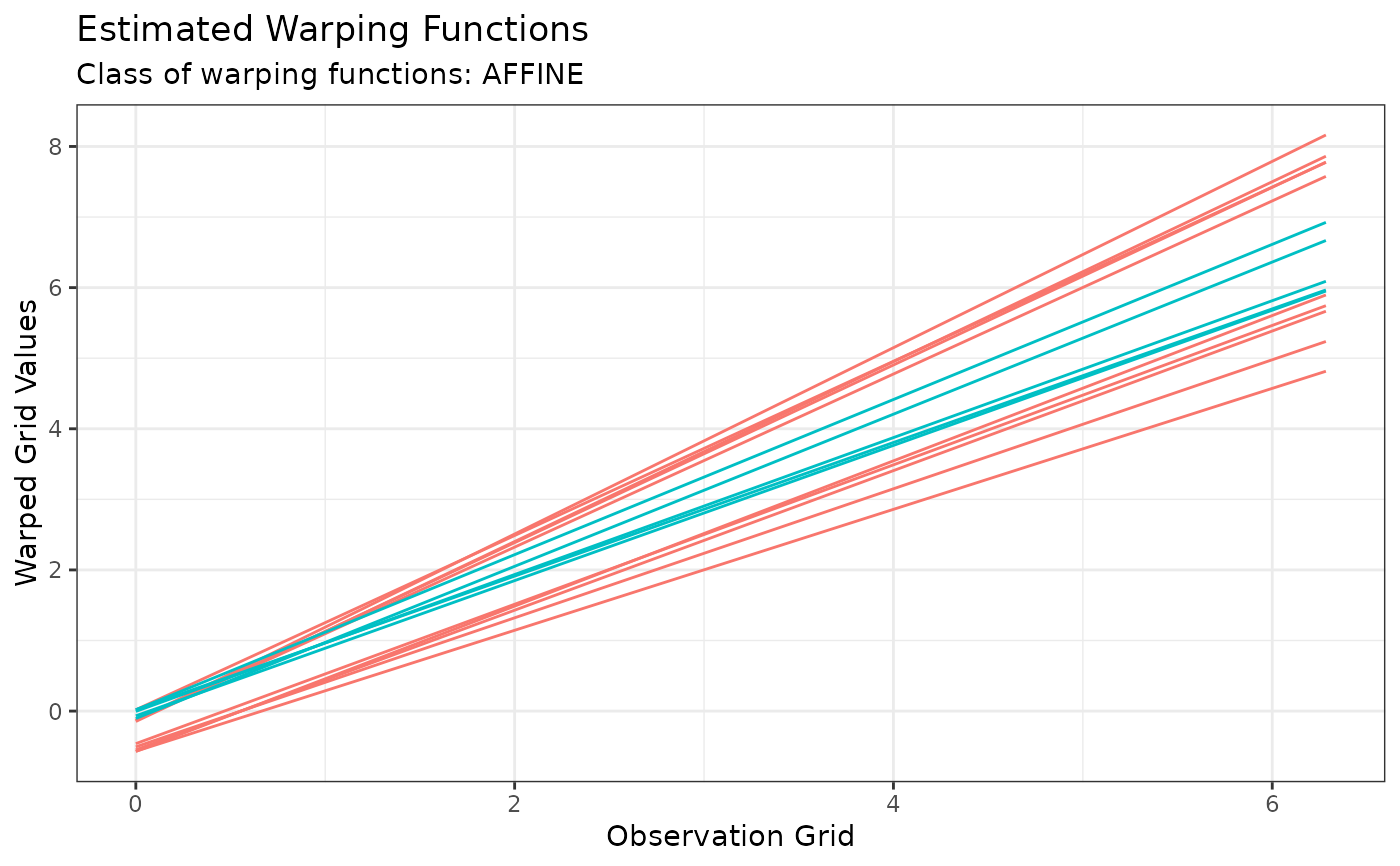
 # Or the estimated warping functions with:
plot(out, type = "phase")
#> Warning: row names were found from a short variable and have been discarded
# Or the estimated warping functions with:
plot(out, type = "phase")
#> Warning: row names were found from a short variable and have been discarded