Performs density-based clustering for functional data with amplitude and phase separation

This function extends DBSCAN to functional data. It includes the possibility to separate amplitude and phase information.

Usage

fdadbscan(
  x,
  y,
  is_domain_interval = FALSE,
  transformation = c("identity", "srsf"),
  warping_class = c("none", "shift", "dilation", "affine", "bpd"),
  centroid_type = "mean",
  metric = c("l2", "normalized_l2", "pearson"),
  cluster_on_phase = FALSE,
  use_verbose = FALSE,
  warping_options = c(0.15, 0.15),
  maximum_number_of_iterations = 100L,
  number_of_threads = 1L,
  parallel_method = 0L,
  distance_relative_tolerance = 0.001,
  use_fence = FALSE,
  check_total_dissimilarity = TRUE,
  compute_overall_center = FALSE
)

Arguments

x: A numeric vector of length \(M\) or a numeric matrix of shape \(N \times M\) or an object of class funData::funData. If a numeric vector or matrix, it specifies the grid(s) of size \(M\) on which each of the \(N\) curves have been observed. If an object of class funData::funData, it contains the whole functional data set and the y argument is not used.
y: Either a numeric matrix of shape \(N \times M\) or a numeric array of shape \(N \times L \times M\) or an object of class fda::fd. If a numeric matrix or array, it specifies the \(N\)-sample of \(L\)-dimensional curves observed on grids of size \(M\). If an object of class fda::fd, it contains all the necessary information about the functional data set to be able to evaluate it on user-defined grids.
is_domain_interval: A boolean specifying whether the sample of curves is defined on a fixed interval. Defaults to FALSE.
transformation: A string specifying the transformation to apply to the original sample of curves. Choices are no transformation (transformation = "identity") or square-root slope function transformation = "srsf". Defaults to "identity".
warping_class: A string specifying the class of warping functions. Choices are no warping (warping_class = "none"), shift y = x + b (warping_class = "shift"), dilation y = ax (warping_class = "dilation"), affine y = ax + b (warping_class = "affine") or boundary-preserving diffeomorphism (warping_class = "bpd"). Defaults to "none".
centroid_type: A string specifying the type of centroid to compute. Choices are "mean", "median" "medoid", "lowess" or "poly". Defaults to "mean". If LOWESS appproximation is chosen, the user can append an integer between 0 and 100 as in "lowess20". This number will be used as the smoother span. This gives the proportion of points in the plot which influence the smooth at each value. Larger values give more smoothness. The default value is 10%. If polynomial approximation is chosen, the user can append an positive integer as in "poly3". This number will be used as the degree of the polynomial model. The default value is 4L.
metric: A string specifying the metric used to compare curves. Choices are "l2", "normalized_l2" or "pearson". If transformation == "srsf", the metric must be "l2" because the SRSF transform maps absolutely continuous functions to square-integrable functions. If transformation == "identity" and warping_class is either dilation or affine, the metric cab be either "normalized_l2" or "pearson". The L2 distance is indeed not dilation-invariant or affine-invariant. The metric can also be "l2" if warping_class == "shift". Defaults to "l2".
cluster_on_phase: A boolean specifying whether clustering should be based on phase variation or amplitude variation. Defaults to FALSE which implies amplitude variation.
use_verbose: A boolean specifying whether the algorithm should output details of the steps to the console. Defaults to FALSE.
warping_options: A numeric vector supplied as a helper to the chosen warping_class to decide on warping parameter bounds. This is used only when warping_class != "srsf".
maximum_number_of_iterations: An integer specifying the maximum number of iterations before the algorithm stops if no other convergence criterion was met. Defaults to 100L.
number_of_threads: An integer value specifying the number of threads used for parallelization. Defaults to 1L. This is used only when warping_class != "srsf".
parallel_method: An integer value specifying the type of desired parallelization for template computation, If 0L, templates are computed in parallel. If 1L, parallelization occurs within a single template computation (only for the medoid method as of now). Defaults to 0L. This is used only when warping_class != "srsf".
distance_relative_tolerance: A numeric value specifying a relative tolerance on the distance update between two iterations. If all observations have not sufficiently improved in that sense, the algorithm stops. Defaults to 1e-3. This is used only when warping_class != "srsf".
use_fence: A boolean specifying whether the fence algorithm should be used to robustify the algorithm against outliers. Defaults to FALSE. This is used only when warping_class != "srsf".
check_total_dissimilarity: A boolean specifying whether an additional stopping criterion based on improvement of the total dissimilarity should be used. Defaults to TRUE. This is used only when warping_class != "srsf".
compute_overall_center: A boolean specifying whether the overall center should be also computed. Defaults to FALSE. This is used only when warping_class != "srsf".

Value

An object of class caps.

Examples

#----------------------------------
# Extracts 15 out of the 30 simulated curves in `simulated30_sub` data set
idx <- c(1:5, 11:15)
x <- simulated30_sub$x[idx, ]
y <- simulated30_sub$y[idx, , ]

#----------------------------------
# Runs an HAC with affine alignment, searching for 2 clusters
out <- fdadbscan(
  x = x,
  y = y,
  warping_class = "affine",
  metric = "normalized_l2"
)

#----------------------------------
# Then visualize the results
# Either with ggplot2 via ggplot2::autoplot(out)
# or using graphics::plot()
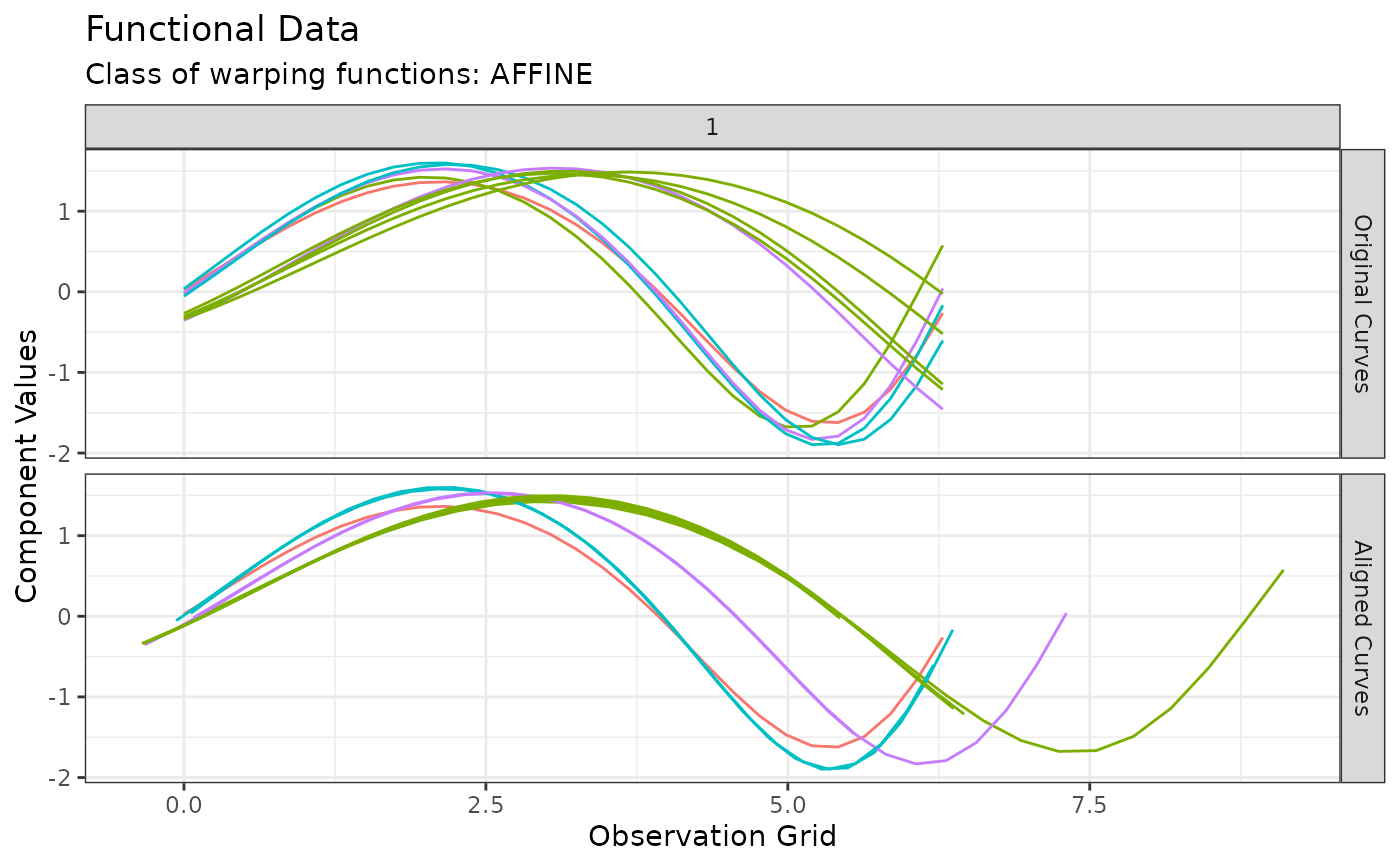
# You can visualize the original and aligned curves with:
plot(out, type = "amplitude")

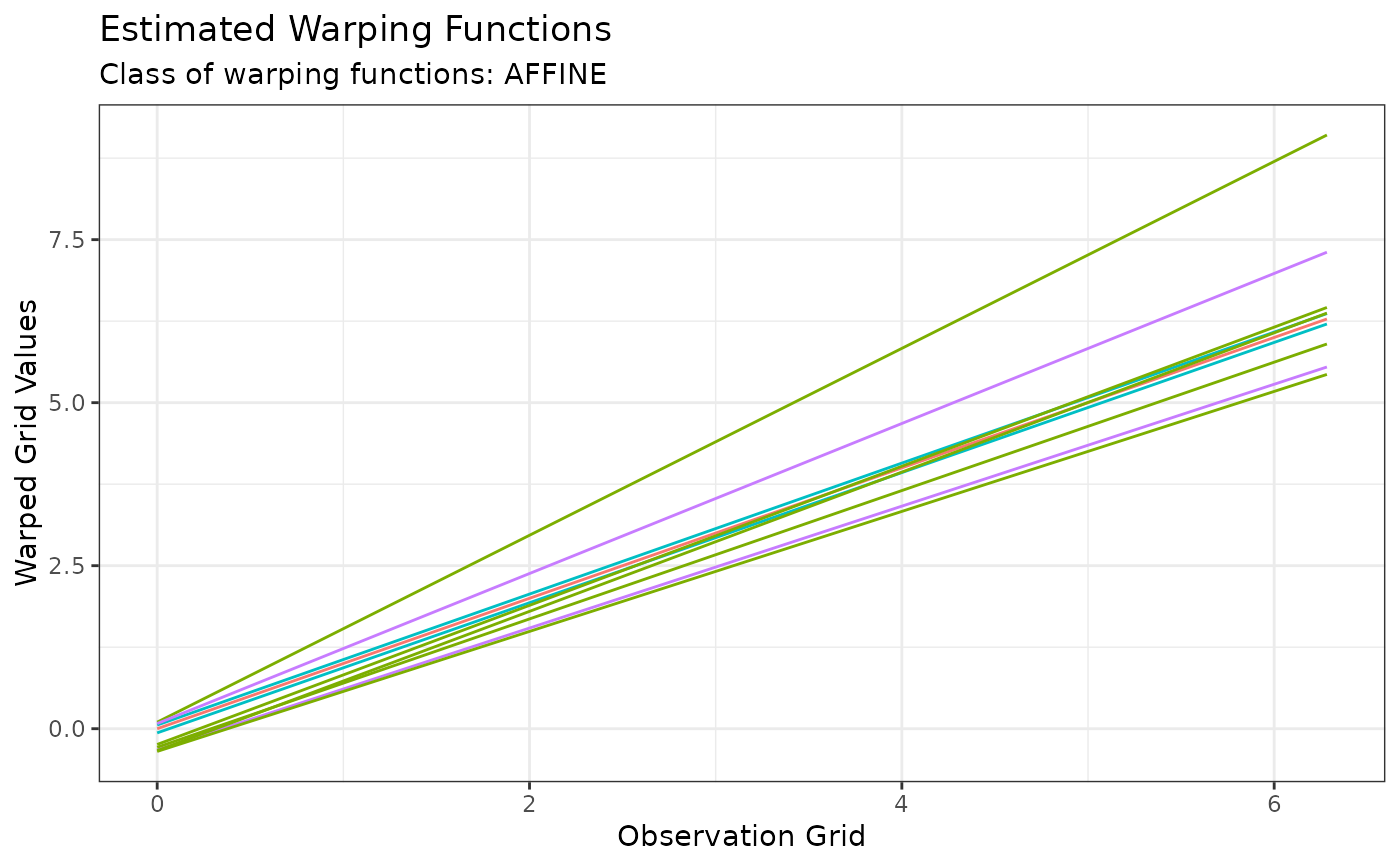
# Or the estimated warping functions with:
plot(out, type = "phase")