R, un catalyseur d’interdisciplinarité

Tour d’horizon du projet eGait sur l’analyse de la marche

L. Bellanger

Lab-STICC, UMR CNRS 6285, Institut Universitaire de Technologie de Vannes, France

M. Simonot

Department of Mathematics Jean Leray, UMR CNRS 6629, Nantes University, Ecole Centrale de Nantes, France

A. Stamm

Department of Mathematics Jean Leray, UMR CNRS 6629, Nantes University, Ecole Centrale de Nantes, France

2025-05-21

Application of R in medicine, pharma and biotech

Maths research for health sciences

Feature	Mathematics Research	Mathematics in Health Sciences
Personnel	Mathematicians, statisticians, software developers	Interdisciplinary team incl. medical staff, engineers, data managers, mathematicians
Interactions	Internal discussions among mathematical experts	Regular cross-disciplinary meetings, clinical-mathematical interface
Core Tasks	Theoretical development, proofs, algorithmic implementation	Balanced between theory and practical implementation, clinical validation
Project Goals	Advance mathematical theory and methodology	Solve specific clinical problems, improve patient care
Validation	Mathematical proofs, simulation studies	Clinical trials, real-world testing, practitioner feedback
Deliverables	Academic papers, theoretical results, software packages	Clinical tools, decision support systems, protocols, training materials
Communication	Technical mathematical language	Translation between technical and clinical language
Impact Metrics	Academic citations, theoretical advancement	Clinical outcomes, practical utility, patient benefit

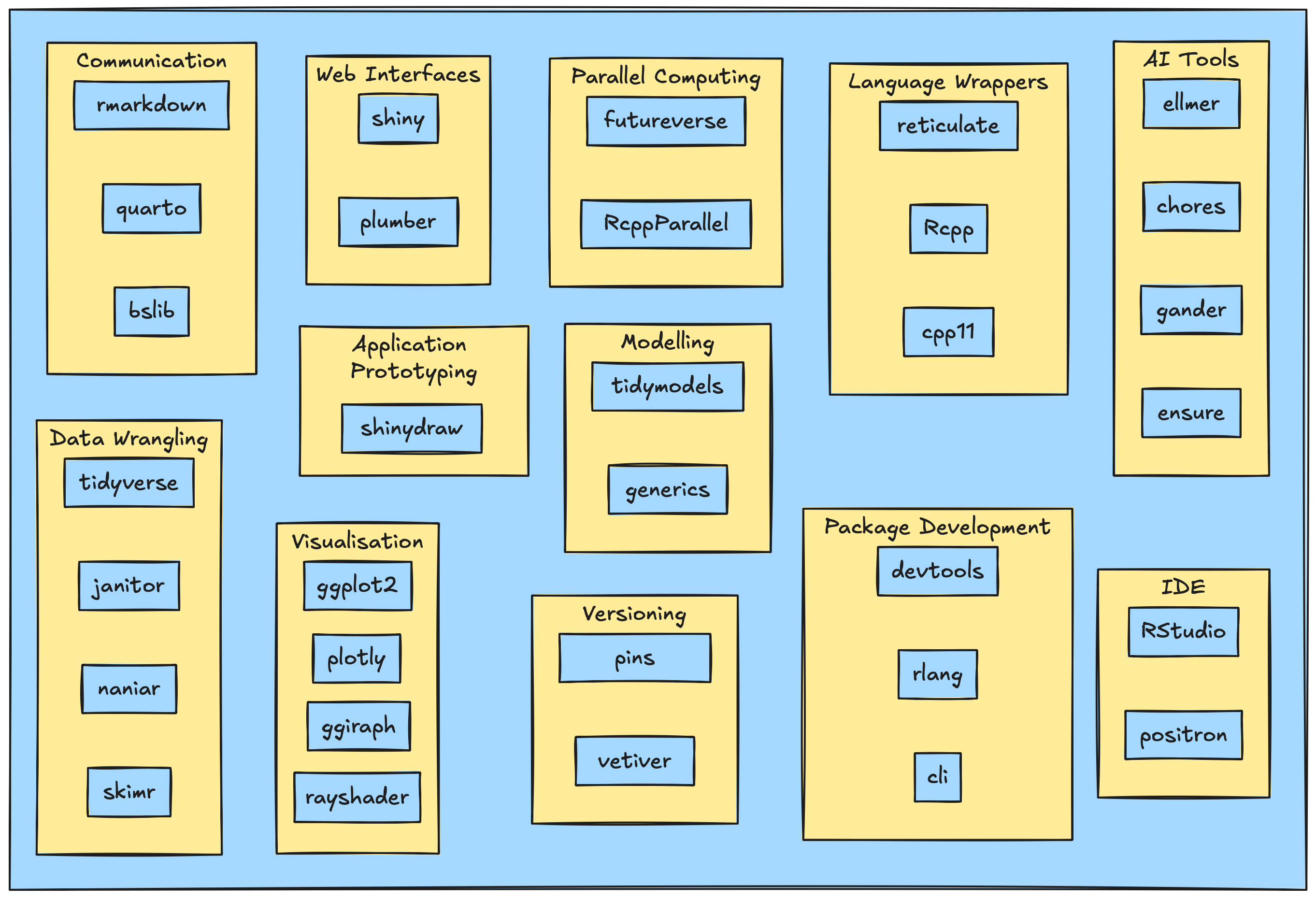
Why R?

Some reasons to use R

• Common language between statisticians, data scientists and biostatisticians
• Used in academia and industry
• Open-source, free, well-curated CRAN repo, well-documented
• Lots of recent efforts to improve the R ecosystem:

The eGait project

Gait analysis of body part orientation over time

The eGait project

Key numbers in France

Multiple Sclerosis

100,000

Parkinson's disease

160,000

Elderly (> 65 years)

14,851,943

Key observations

• Gait impairment: major symptom impacting quality of daily life;
• Clinical gait assessment mostly qualitative and biased:
  • Only in a constrained environment (as opposed to free-living environment);
  • Mainly based on the expertise of the clinician;
  • Quantitative measures boil down to timing a given walking distance.
• Need for a quantitative, objective, and reproducible assessment of gait.

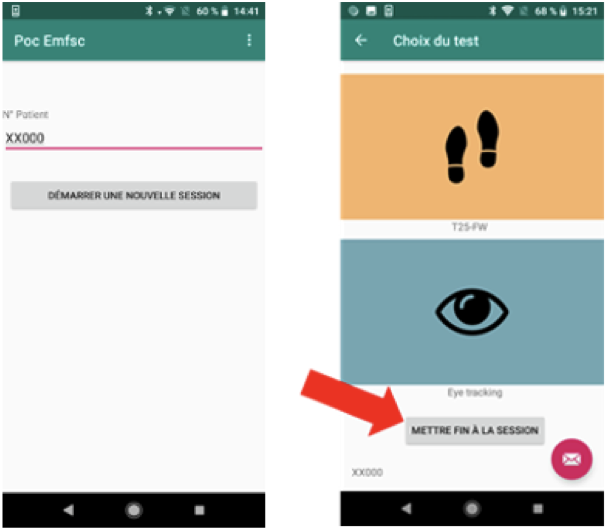
The eGait device

• An inertial measurement unit (IMU): defines the data (orientation e.g. 3D rotations over time),
• A smartphone application: collects the data,
• Statistical methods for rotation-valued functional data: analyses the data

(a) Data recording

(b) Smartphone & App

(c) Rotation data

Figure 1: The eGait device (Brard et al. 2022; Drouin 2022; Drouin et al. 2023; Ballante et al. 2023).

Rotation data from the sensor

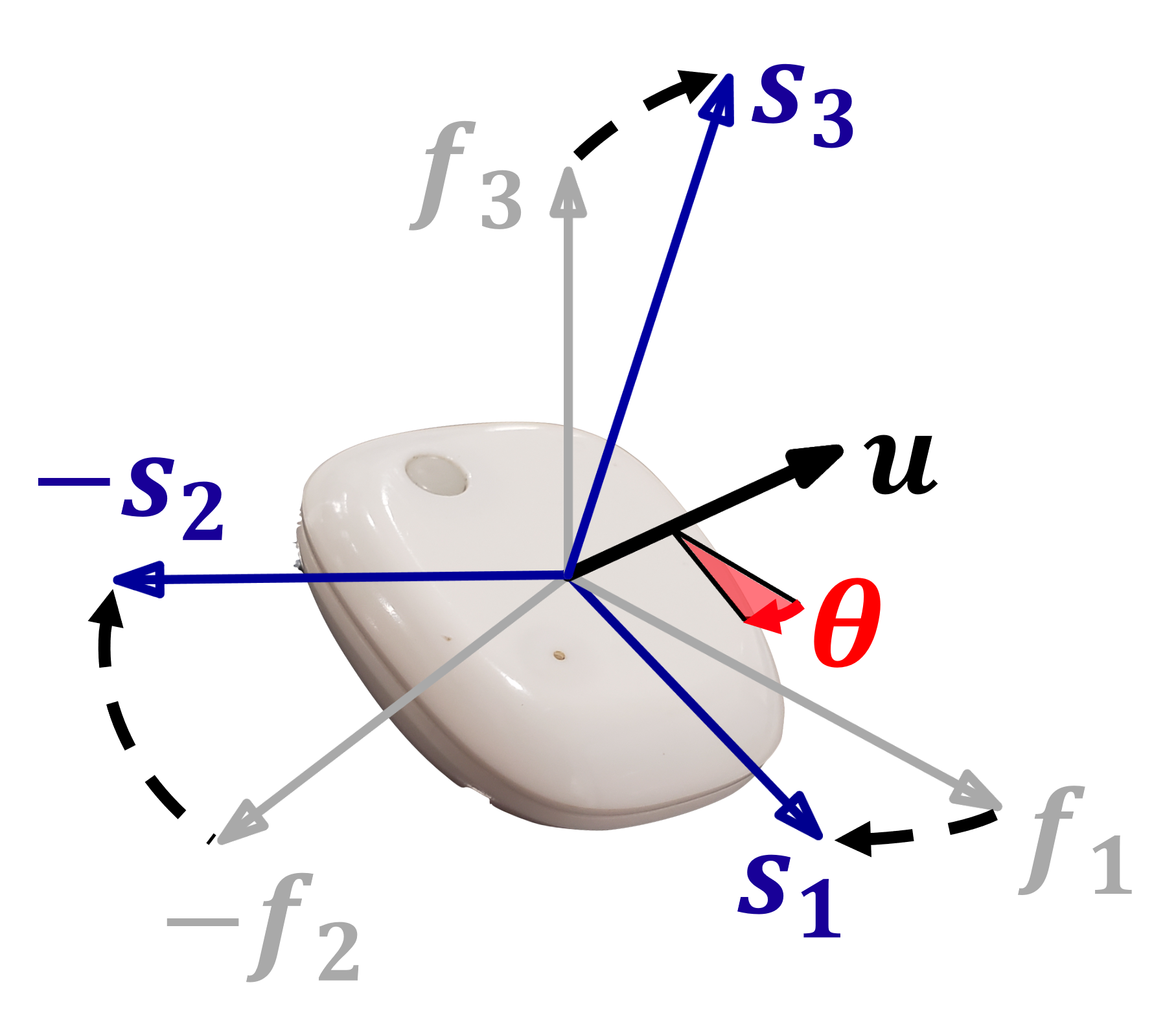
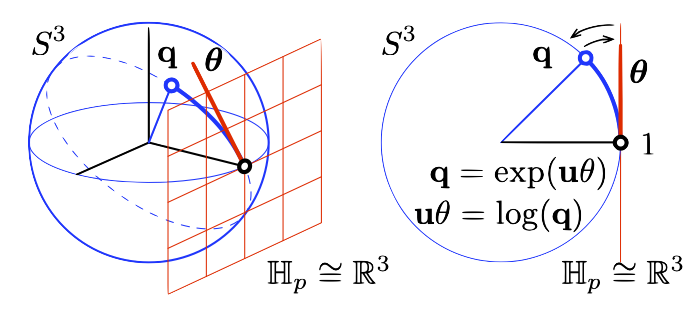
Unit quaternion

A unit quaternion \(\mathbf{q} = (q_w, q_x, q_y, q_z)^\top \in \mathbb{R}^4\) encodes a rotation of angle \(\theta\) around the axis \(\mathbf{u}\) as: \[ \begin{aligned} \mathbf{q} &= q_w + q_x \mathbf{i} + q_y \mathbf{j} + q_z \mathbf{k} \\ &= \cos \left( \frac{\theta}{2} \right) + (u_x \mathbf{i} + u_y \mathbf{j} + u_z \mathbf{k}) \sin \left( \frac{\theta}{2} \right), \end{aligned} \] with \(\mathbf{i}^2 = \mathbf{j}^2 = \mathbf{k}^2 = \mathbf{i} \mathbf{j} \mathbf{k} = -1\).

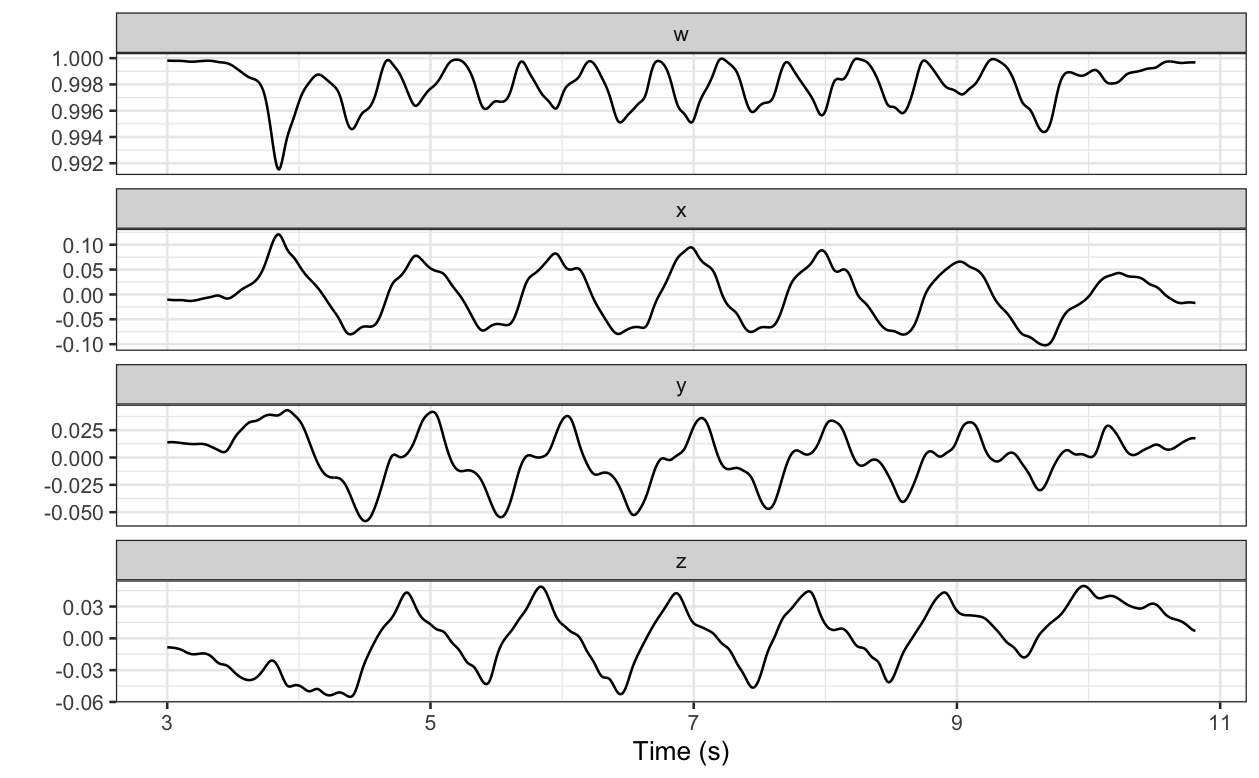
Raw data collected by the eGait device:

• Represents the hip rotation over time (Drouin 2022);
• In the form of a unit quaternion time series.

Figure 2: Angle–axis representation¹.

Figure 3: An example of a unit quaternion time series measured by the eGait device.

1. Taken from (Drouin et al. 2023).

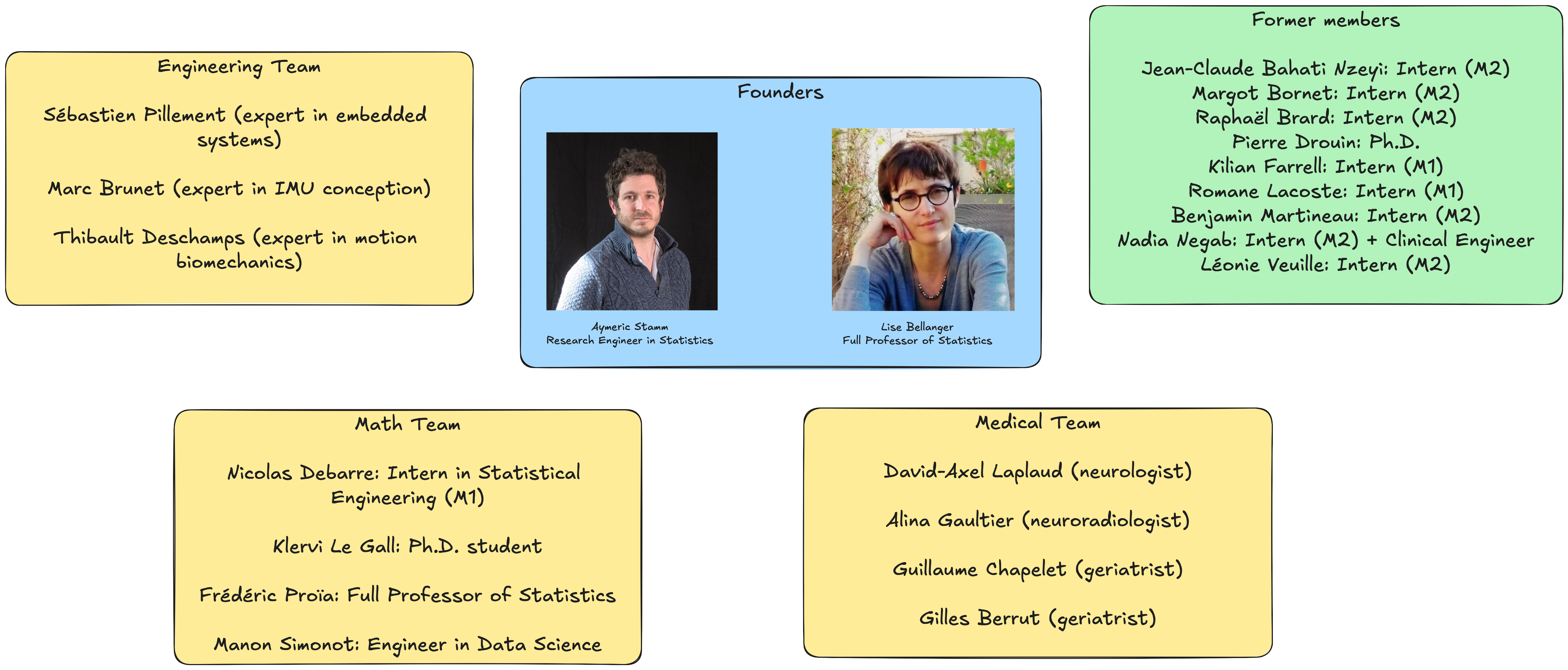
The Team

 

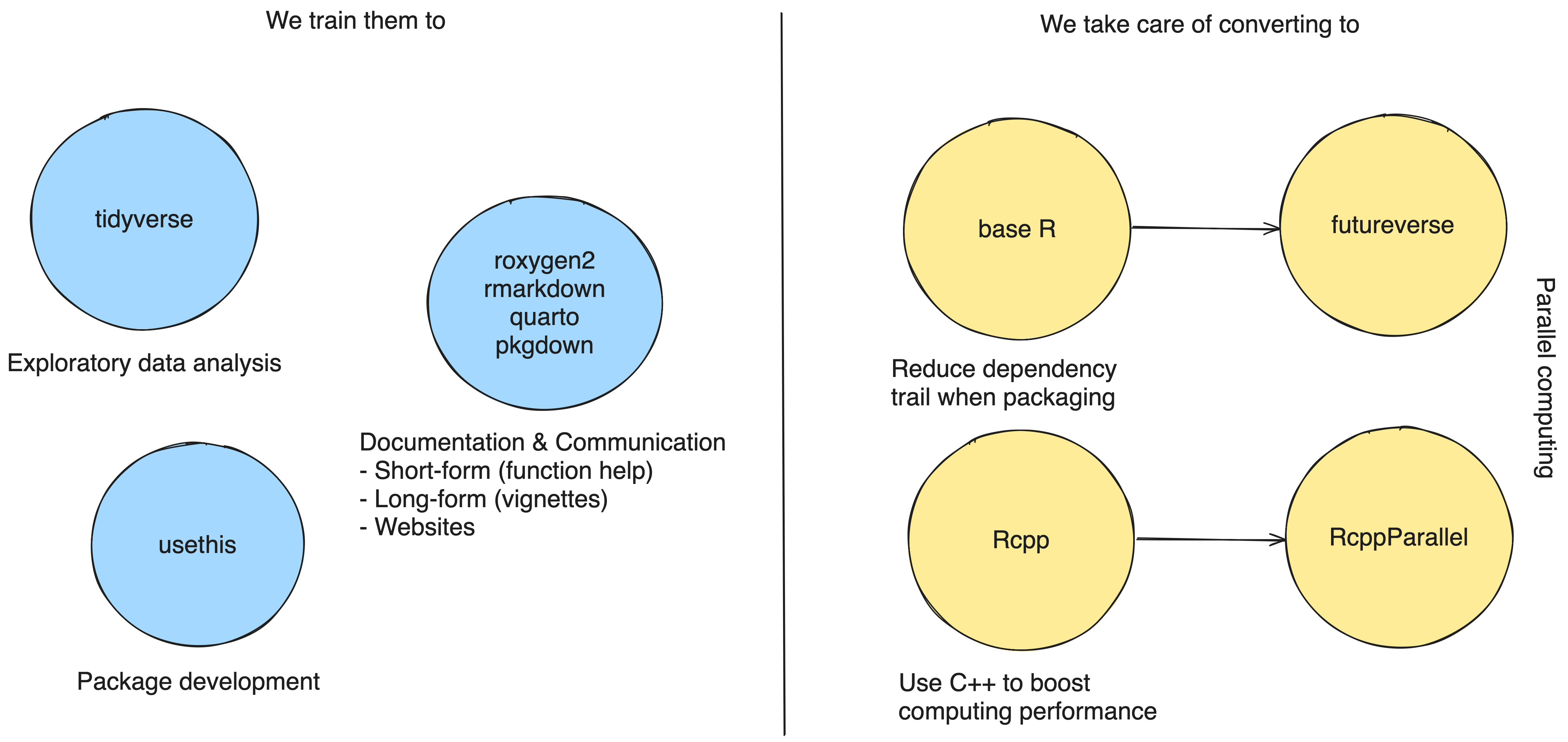
Challenge 1: handling contributions from math students

Math students

• trained to become data scientists;
• should be able to use R for exploratory data analysis and modeling;
• should be able to use quarto for reproducible research;
• no knowledge of R package development;
• no practice of redacting documentation
• no knowledge of compiled languages
• no knowledge of parallel computing

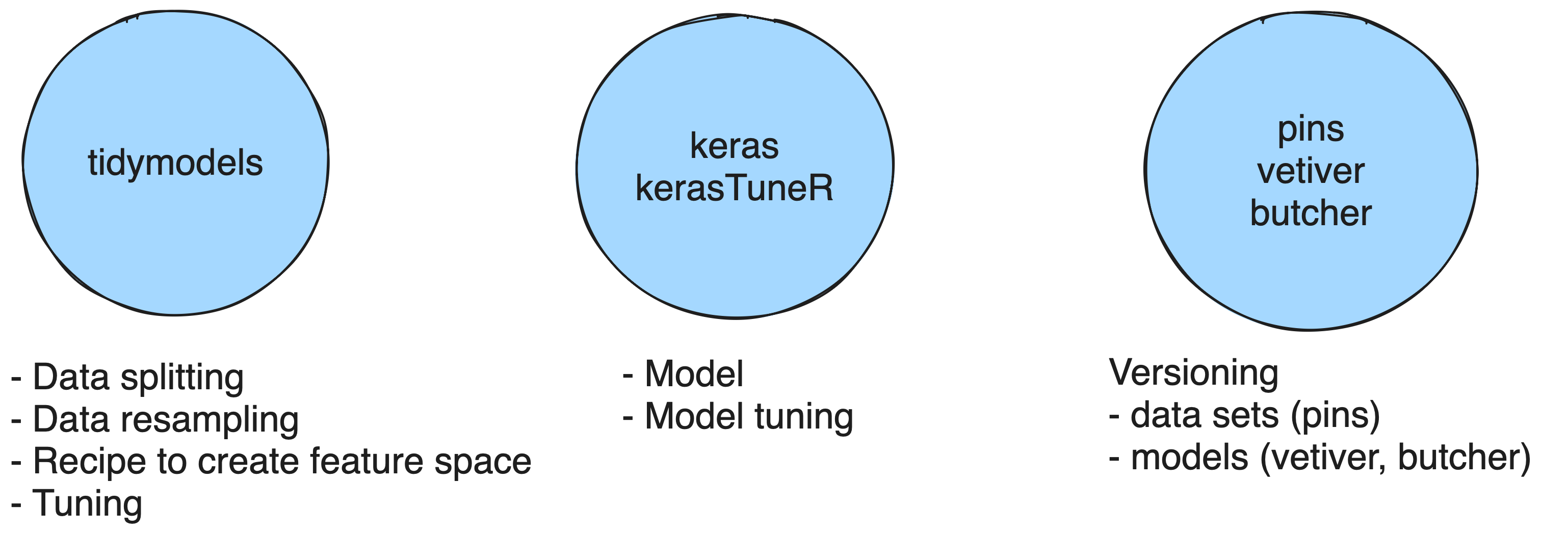
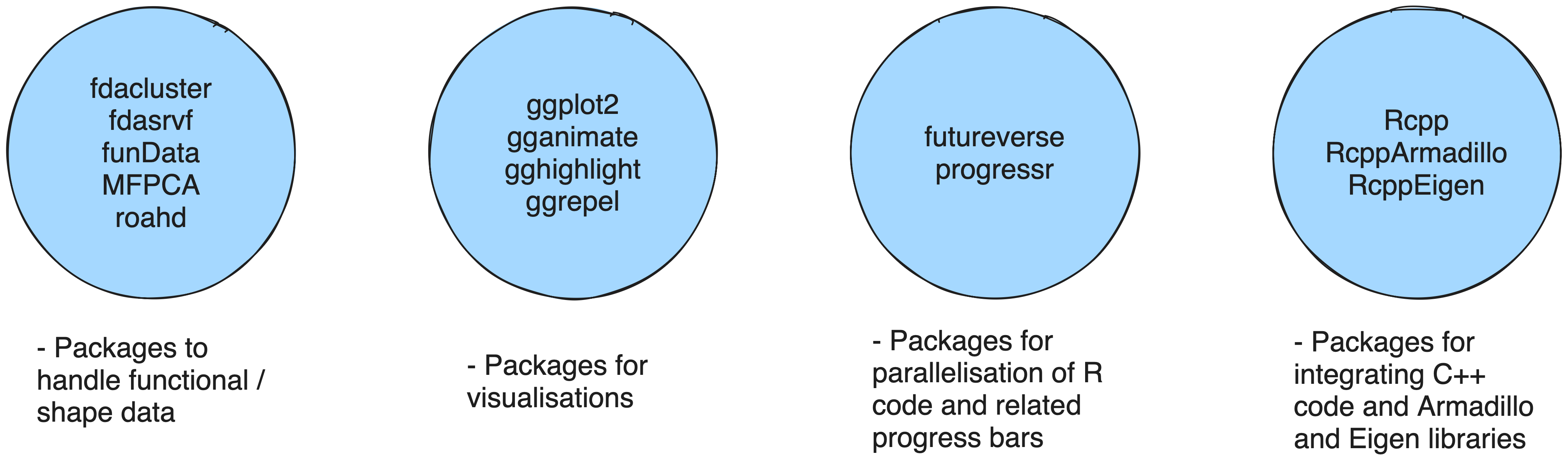
R to the rescue

 

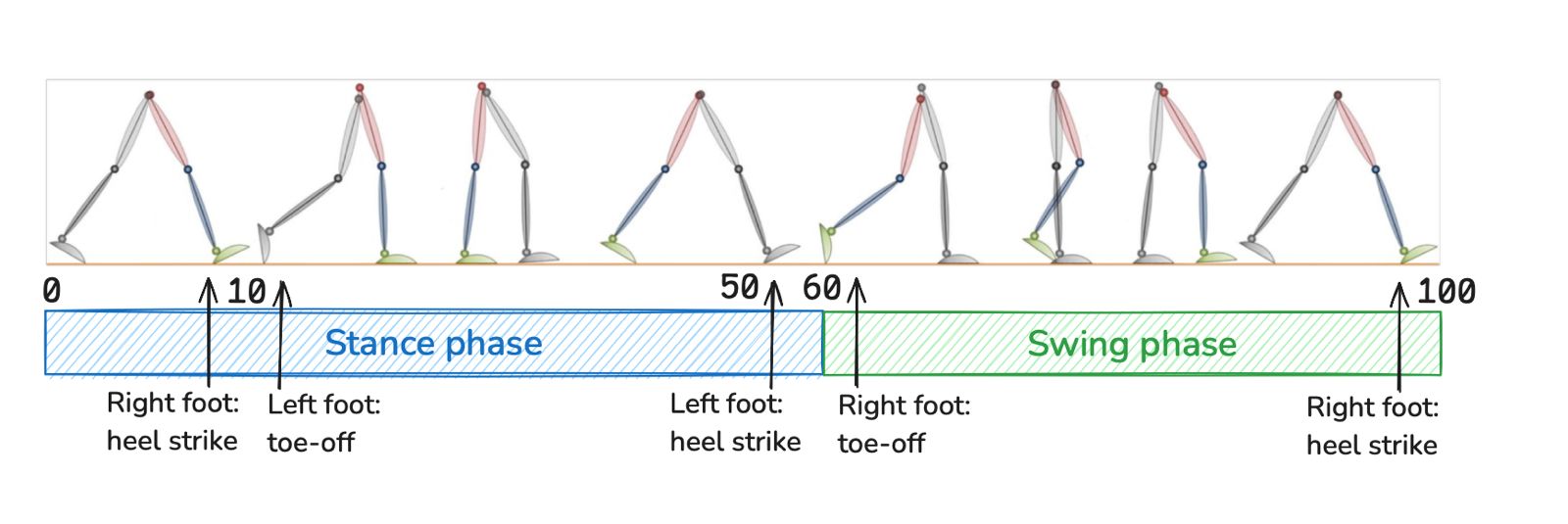
Gait analysis

Gait cycle

Set of movements accomplished in between two consecutive heel strikes of the same foot on the ground.

Figure 4: The different phases of a typical gait cycle¹.

 

Segmentation points:

Heel strikes of right foot.

\(\Longrightarrow\) Segmentation of the raw signal into gait cycles.

1. Annotated from Jaquelin Perry’s image on Wikipedia.

Challenge 2: Segmentation of gait cycles

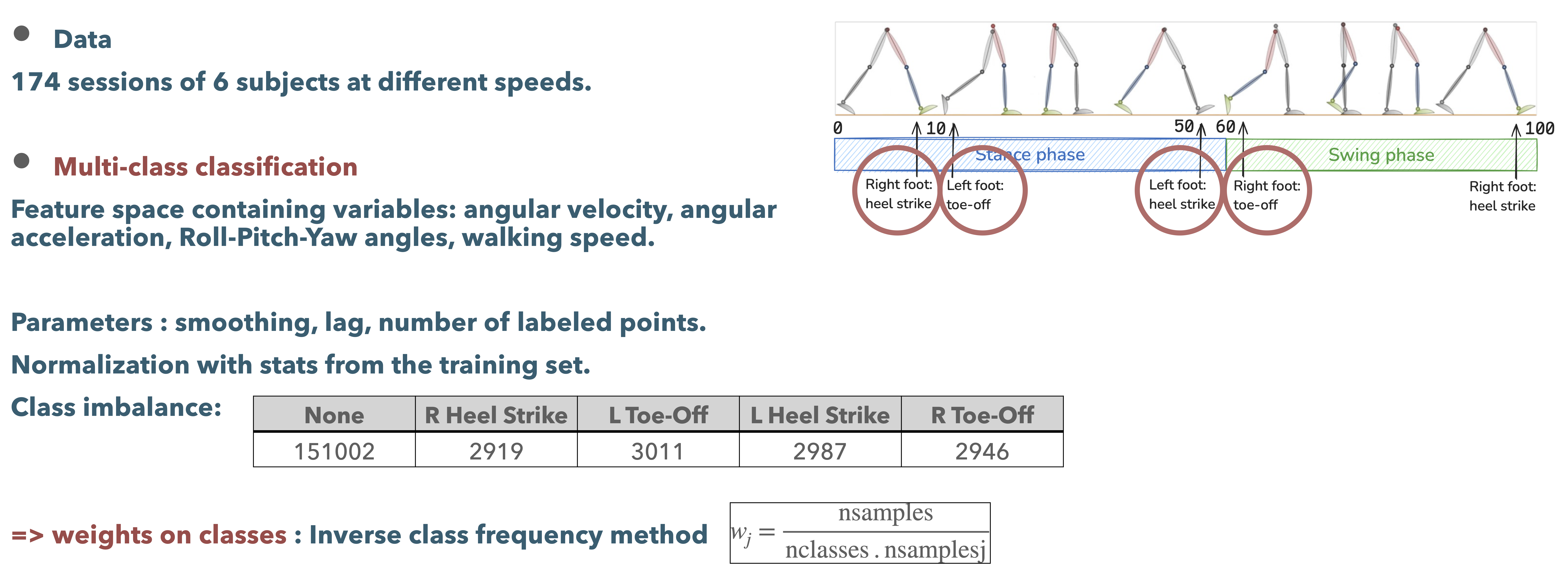
A neural network model

Time points as observations

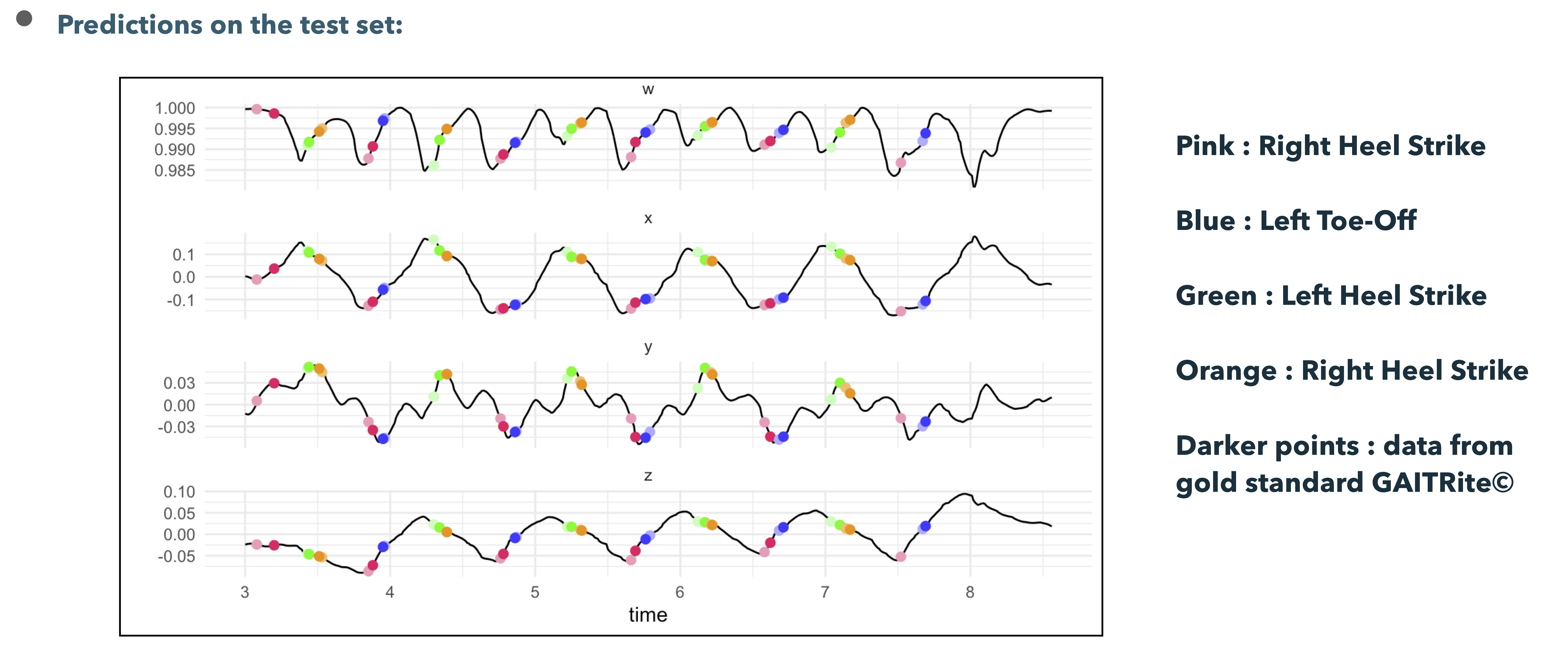
We view the segmentation of gait cycles as a problem of classification of time points into 5 classes: Right Heel Strike, Left Heel Strike, Right Toe Off, Left Toe Off and No Event.

We collected data on a reference treadmill which provides ground truth for the segmentation via pressure sensors.

Result on test set

 

R to the rescue

 

Functional Data Analysis

Handling non-Euclidean geometry

Lie groups

Definition 1 (Smooth manifold) A smooth or differentiable manifold is a topological space that locally resembles linear space.

Figure 5: A manifold \(\mathcal{M}\) and the vector space \(T_\mathcal{X} \mathcal{M}\) tangent at point \(\mathcal{X}\). The velocity element \(\dot{\mathcal{X}}\) does not belong to the manifold but to the tangent space (Sola, Deray, and Atchuthan 2018).

Lie groups

Definition 2 (Group) A group is a set \(\mathcal{G}\), with composition operation \(\circ\), that, for elements \(\mathcal{X}, \mathcal{Y}, \mathcal{Z} \in \mathcal{G}\), satisfies the following axioms:

• Closure under \(\circ\): \(\mathcal{X} \circ \mathcal{Y} \in \mathcal{G}\)
• Identity \(\mathcal{E}\): \(\mathcal{E} \circ \mathcal{X} = \mathcal{X} \circ \mathcal{E} = \mathcal{X}\)
• Inverse \(\mathcal{X}^{-1}\): \(\mathcal{X}^{-1} \circ \mathcal{X} = \mathcal{X} \circ \mathcal{X}^{-1} = \mathcal{E}\)
• Associativity: \((\mathcal{X} \circ \mathcal{Y}) \circ \mathcal{Z} = \mathcal{X} \circ (\mathcal{Y} \circ \mathcal{Z})\)

Definition 3 (Lie group) A Lie group is a smooth manifold whose elements satisfy the group axioms.

Figure 6: Representation of a Lie group and its Lie algebra. The Lie algebra \(T_\mathcal{E} \mathcal{M}\) (red plane) is the tangent space to the Lie group \(\mathcal{M}\) (blue sphere) at the identity \(\mathcal{E}\) (Sola, Deray, and Atchuthan 2018).

The Lie group \(S^3\) of unit quaternions

Figure 7: The \(S^3\) manifold is a unit 3-sphere (blue) in the 4-space of quaternions \(\mathbb{H}\), where the unit quaternions \(\mathbf{q}^\star \mathbf{q} = 1\) live. The Lie algebra is the space of pure imaginary quaternions \(ix + jy + kz \in \mathbb{H}_p\), isomorphic to the hyperplane \(\mathbb{R}^3\) (red grid), and any other tangent space \(T S^3\) is also isomorphic to \(\mathbb{R}^3\) (Sola, Deray, and Atchuthan 2018).

Vectors \(\mathbf{x} = (0, x_1, x_2, x_3) = 0 + ix_1 + jx_2 + kx_3\) rotate in 3D space by an angle \(\theta\) around the unit axis \(\mathbf{u}\) through the double quaternion product \(\mathbf{x}^\prime = \mathbf{q} \mathbf{x} \mathbf{q}^\star\).

From \(S^3\)- to \(\mathbb{R}^3\)-valued functional data

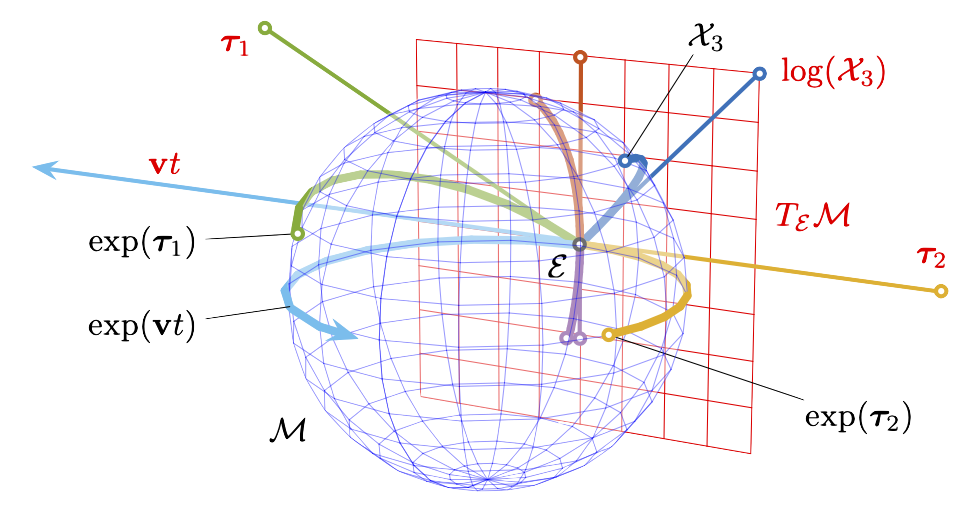
Original manifold \(\mathbb{S}^3\)

\[ \scriptsize{ \begin{array}{rccc} \mathbf{q}: & [0,1] & \to & \mathbb{S}^3 \\ & s & \mapsto & \mathbf{q}(s) \end{array} } \]

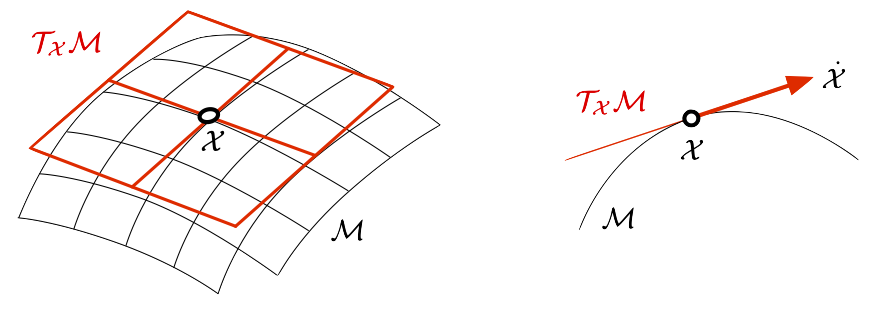
Tangent space \(\mathcal{T}\mathbb{S}^3 \approx \mathbb{R}^3\)

\[ \scriptsize{ \begin{array}{rccc} \mathbf{t}: & [0,1] & \to & \mathbb{R}^3 \\ & s & \mapsto & \log(\mathbf{q}(s)) = (\theta(s) / 2) \mathbf{v}(s) \end{array} } \]

Metric space

Which distance should we use?

Square-root velocity function (SRVF) space \(L^2 \left( [0, 1], \mathbb{R}^3 \right)\) (Kurtek et al. 2012; Tucker, Wu, and Srivastava 2013; Srivastava and Klassen 2016)

\[ \scriptsize{ \begin{array}{rccc} \mathbf{v}: & [0,1] & \to & \mathbb{R}^3 \\ & s & \mapsto & \begin{cases} \frac{\mathbf{t}^\prime(s))}{\sqrt{\| \mathbf{t}^\prime(s)) \|}} & \text{if } \mathbf{t}^\prime(s) \neq 0 \\ 0 & \text{otherwise} \end{cases} \end{array} } \]

Elastic shape metrics

• The SRVF space is by construction invariant by translation:

\[ d(\mathbf{t}_1, \mathbf{t}_2) = \left\| \mathbf{v}_1 - \mathbf{v}_2 \right\|_{L^2} \quad \mbox{and} \quad d(\mathbf{t}_1 + \mathbf{x}_0, \mathbf{t}_2 + \mathbf{x}_0) = d(\mathbf{t}_1, \mathbf{t}_2) \]

• We can use suitable metrics to add further geometric invariants:

Geometric invariant	Distance (all isometric)
Warping	\(d(\mathbf{t}_1, \mathbf{t}_2) = \min_{\gamma \in \Gamma} \left\| \mathbf{v}_1 - (\mathbf{v}_2 \circ \gamma) \sqrt{\dot{\gamma}} \right\|_{L^2}\)
Orientation	\(d(\mathbf{t}_1, \mathbf{t}_2) = \min_{R \in \mathrm{SO}(3)} \left\| \mathbf{v}_1 - R \mathbf{v}_2 \right\|_{L^2}\)
Scale	\(d(\mathbf{t}_1, \mathbf{t}_2) = \left\| \frac{\mathbf{v}_1}{\| \mathbf{v}_1 \|_{L_2}} - \frac{\mathbf{v}_2}{\| \mathbf{v}_2 \|_{L_2}} \right\|_{L^2}\)

\[ \Gamma = \{ \gamma : [0,1] \to [0,1] | \gamma(0) = 0, \gamma(1) = 1, 0 < \dot{\gamma} < +\infty \} \]

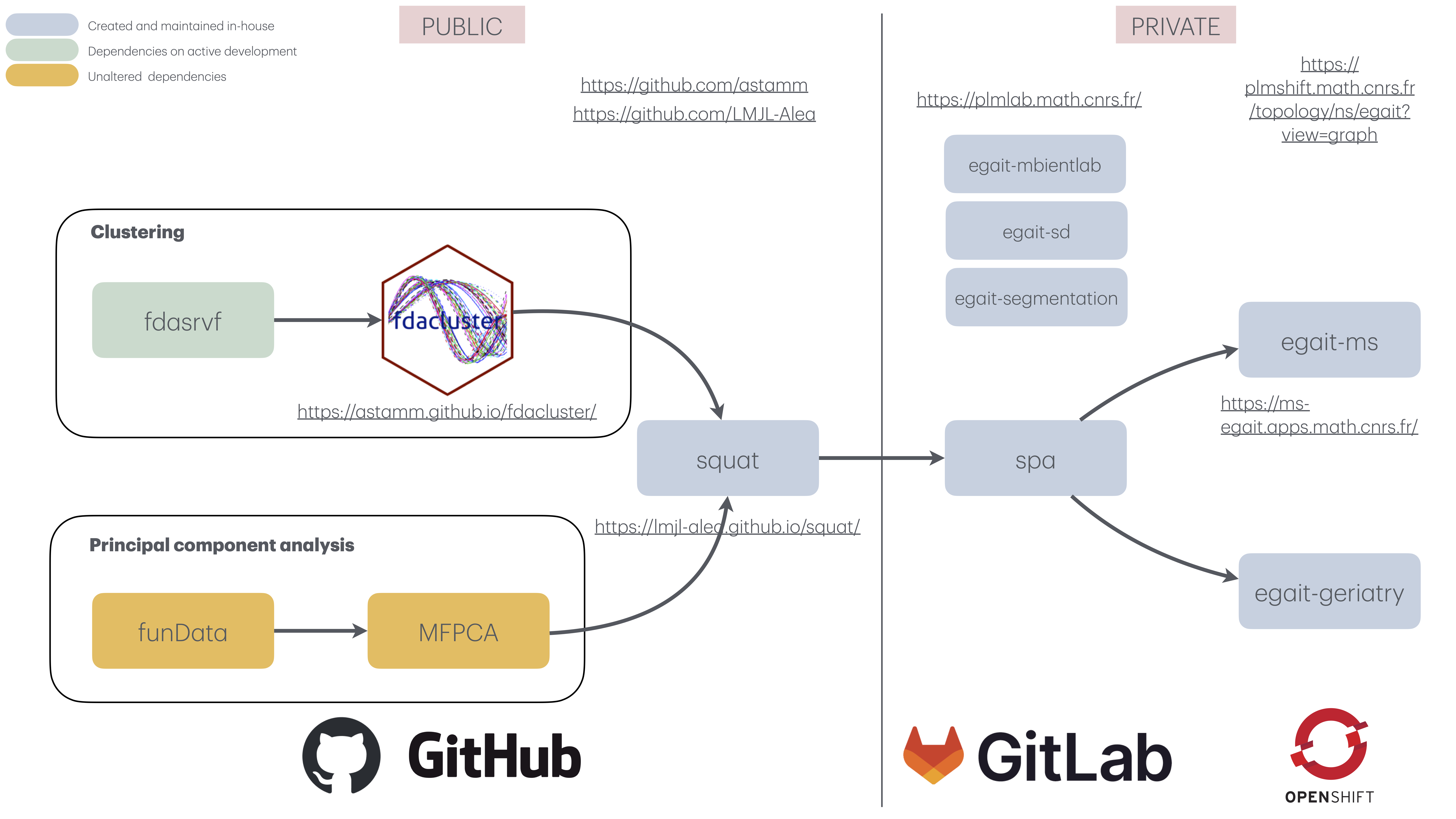
Challenge 3: Provide tools for easy statistical analysis of QTS samples

The {squat} package

QTS Manipulation

• Class qts: centring() around mean quaternion, autoplot(), plot(), +, -, *, inverse_qts().
• Class qts_sample: [, append(), rnorm_qts(), scale(), mean(), median(), autoplot(), plot().
• For both: log(), exp(), normalize(), resample(), smooth(), moving_average(), hemispherize().
• Transformations to other rotation representations.

Clustering - Deps: {fdacluster}, {fdasrvf}, {dbscan} (Sangalli et al. 2010; Vantini 2012)

• S3 impl. of kmeans(), hclust() and dbscan() for qts_sample objects;
• Return an object of class qtsclust;
• S3 impl. of autoplot() and plot() for qtsclust objects for visualization.

PCA - Deps: {MFPCA} (Happ and Greven 2018; Happ-Kurz 2020)

• S3 impl. of prcomp() for qts_sample objects;
• Returns an object of class prcomp_qts;
• S3 impl. of autoplot(), plot() and predict() for prcomp_qts objects.

R to the rescue

 

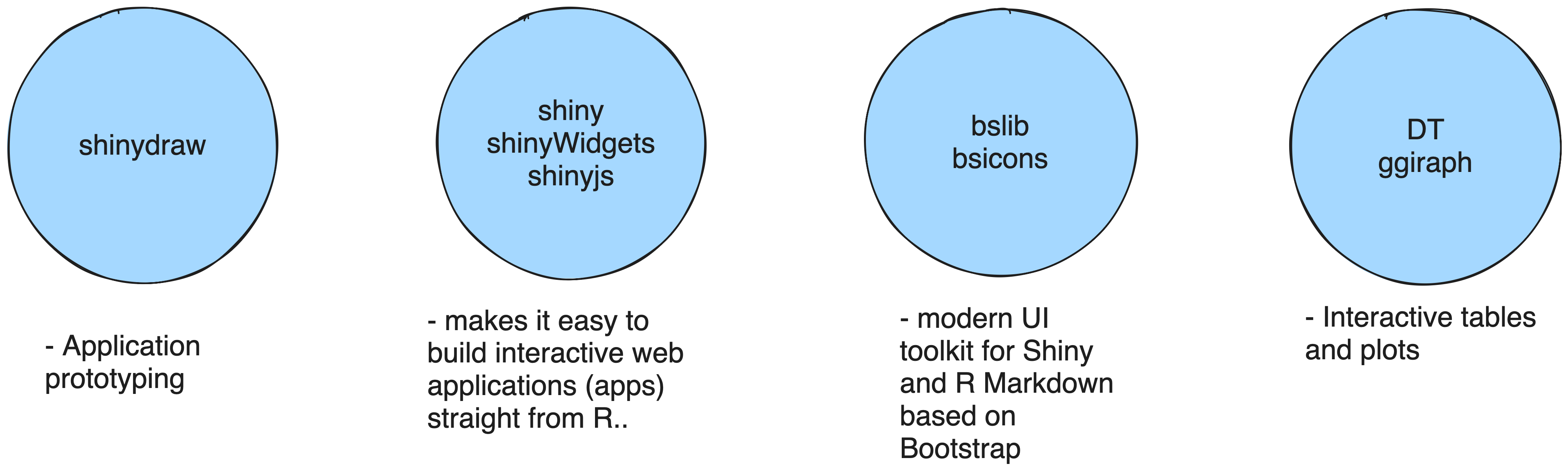
Challenge 4: Communicate with medical experts

Web applications

R to the rescue

 

Wrappin’ up

Conclusion

• Choosing the R language for analysing the data produced by eGait has been a success in fostering collaboration between the medical and statistical communities.
• The squat package provides a solid foundation for statistical analysis of quaternion time series, with a focus on computational efficiency and ease of use.

References

Ballante, Elena, Lise Bellanger, Pierre Drouin, Silvia Figini, and Aymeric Stamm. 2023. “Smoothing Method for Unit Quaternion Time Series in a Classification Problem: An Application to Motion Data.” Scientific Reports 13 (1): 9366.

Brard, Raphaël, Lise Bellanger, Laurent Chevreuil, Fanny Doistau, Pierre Drouin, and Aymeric Stamm. 2022. “A Novel Walking Activity Recognition Model for Rotation Time Series Collected by a Wearable Sensor in a Free-Living Environment.” Sensors 22 (9): 3555.

Drouin, Pierre. 2022. “Amélioration Du Suivi Des Patients Atteints de Maladies Neuro-dégénératives à l’aide d’objets Connectés.” PhD thesis, Nantes Université.

Drouin, Pierre, Aymeric Stamm, Laurent Chevreuil, Vincent Graillot, Laetitia Barbin, Pierre-Antoine Gourraud, David-Axel Laplaud, and Lise Bellanger. 2023. “Semi-Supervised Clustering of Quaternion Time Series: Application to Gait Analysis in Multiple Sclerosis Using Motion Sensor Data.” Statistics in Medicine 42 (4): 433–56.

Happ, Clara, and Sonja Greven. 2018. “Multivariate Functional Principal Component Analysis for Data Observed on Different (Dimensional) Domains.” Journal of the American Statistical Association 113 (522): 649–59.

Happ-Kurz, Clara. 2020. “Object-Oriented Software for Functional Data.” Journal of Statistical Software 93 (5): 1–38. https://doi.org/10.18637/jss.v093.i05.

Kurtek, Sebastian, Anuj Srivastava, Eric Klassen, and Zhaohua Ding. 2012. “Statistical Modeling of Curves Using Shapes and Related Features.” Journal of the American Statistical Association 107 (499): 1152–65.

Sangalli, Laura M, Piercesare Secchi, Simone Vantini, and Valeria Vitelli. 2010. “K-Mean Alignment for Curve Clustering.” Computational Statistics & Data Analysis 54 (5): 1219–33.

Sola, Joan, Jeremie Deray, and Dinesh Atchuthan. 2018. “A Micro Lie Theory for State Estimation in Robotics.” arXiv Preprint arXiv:1812.01537.

Srivastava, Anuj, and Eric P Klassen. 2016. Functional and Shape Data Analysis. Vol. 1. Springer.

Tucker, J Derek, Wei Wu, and Anuj Srivastava. 2013. “Generative Models for Functional Data Using Phase and Amplitude Separation.” Computational Statistics & Data Analysis 61: 50–66.

Vantini, Simone. 2012. “On the Definition of Phase and Amplitude Variability in Functional Data Analysis.” Test 21 (4): 676–96.